Supernumerary Rainbows

Important update: These pages have moved to their own domain at https://rainbowspec.observer, where their information, organization, and graphics have been significantly improved! This page is replaced by my new supernumerary rainbows page.

Supernumerary rainbows are the faint rainbows that can sometimes be seen under the primary rainbow. They occur when the water droplets are smaller than 1mm wide.

At the bottom of my primary rainbows page I illustrate how each color makes a slightly different sized cone of concentrated light (which we see head on as a circle) and how they overlap to form a rainbow. Primary rainbows with supernumeraries overlap very similarly, the concentration of light is simply in banded rings.

This is a rough illustration I made, the next diagram is much more accurate.

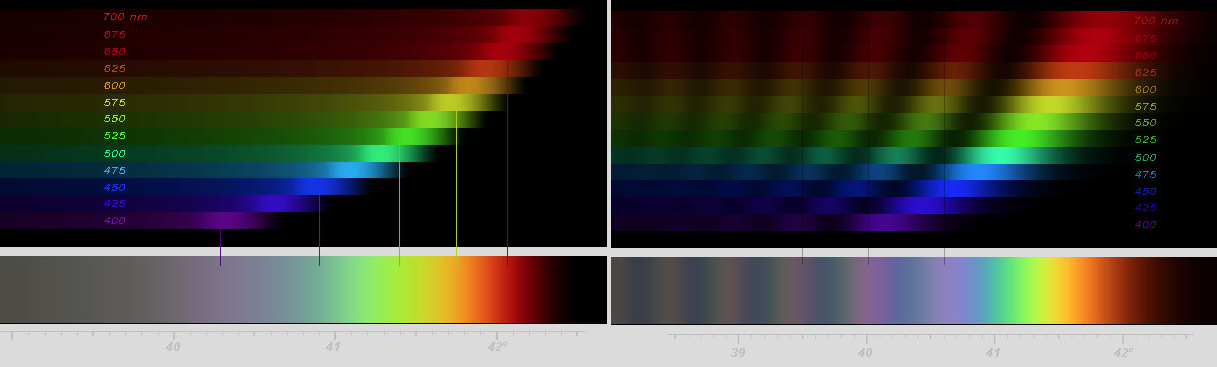
These two simulations show the concentration of each color and how they overlap to form a primary rainbow made from large verus small drops. The left is a primary rainbow formed by larger water droplets, and the right is a primary rainbow with supernumary bands formed from 0.7 mm droplets. Both feature staggered colors, allowing a rainbow to form instead of just white light, but in the supernumary simulation, each wavelength of light is banded. Since the wavelengths are different, each color bands differently, allowing certain colors to show through where others are dark, thus rainbows form. Notably, further from the primary, the bands are more overlapped, creating duller rainbows further out

The smaller the droplets, the wider the supernumary bands are spaced and the brighter they are. Supernumerary bands are most often seen near the top of the rainbow arc, as the water droplets up higher more spherical compared to the lower ones which are flattened slightly from air resistance.

Supernumerary bands are more noticable when the raindrops are uniform in size, if they are too varied, their different banding patterns will overlap and wash each other out.

So why exactly do smaller water droplets form bands of light and large ones don't? Well, wavelengths of light are very small (400nm-700nn) so only drops that are small enough will affect how the waves travel through the drops.

Waves

Light travels in waves, and waves can interact with other waves in what is called interference. They can combine with each other to create larger waves, or cancel each other out to make smaller waves.

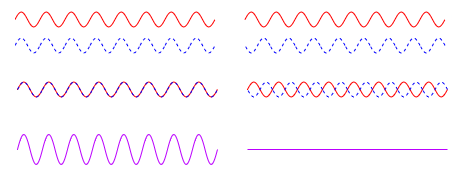
This diagram shows contructive and destructive interference. When the peaks and valleys of two waves line up, they add together, increasing the amplitude of the wave (left). When a peak lines up with another waves valley, they cancel each other out, decreasing the amplitude of the resultant wave (right). Things get a little more complicated when they aren't lined up perfectly like those two situations, but resultant wave will be the sum of the two contributing waves at each point (ex. a peak at 2 lining up with a valley at -2 will equal 0).

Note that this depiction of waves is just an illustration, waves for light do not look like wavy 2D lines, they are more like pulses of energy.

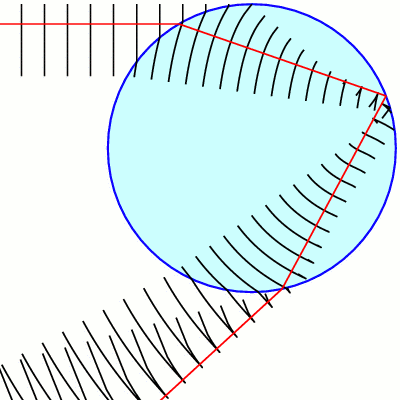
This diagram illustrates waves of light as lines, where the "peaks" of the waves are the lines. this diagram does not distinguish individual rays of light, but countless rays acting together. one line represents a peak of countless rays next to each other.

Most notably is the fact that when the straight waves from the sun hit the curved surface of the drop, they too become curved! The smaller the drop the more severe the curve of the surface is. Large water drops are so large compared to the wavelengths of light that its curved surface is very slight and negligible, like how the horizon of the earth appears flat to us. This is why only small drops give supernumerary bands.

We know that once the exiting rays hit 42 deg from the entrance rays, the light folds back in on itself and flares back upward, making a hard line that forms the primary bow. This is where we get the strange overlap of waves in this diagram.

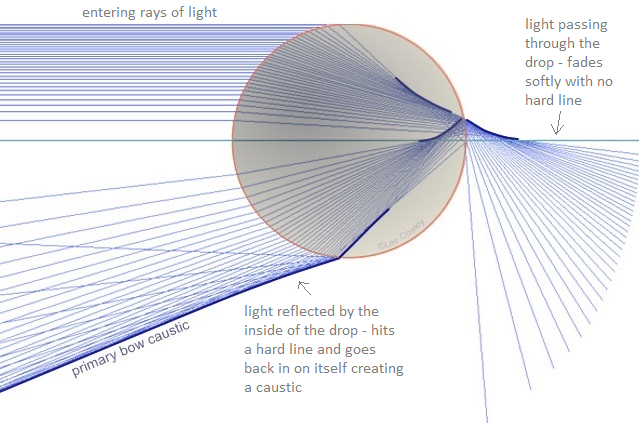
Consider this diagram again, showing how the reflected rays hit a hard line and go back up, overlapping the other reflected rays. This is a ray diagram, with just straight lines, unlike the previous it doesn't show light in its wave form. In wave form we will see an interference pattern.

Here are the exit waves are extended to show how they overlap. Where the curved lines overlap perfectly, showing the same amount of space between the lines as the non-overlapping waves, is where there is constructive interference, the peaks and valleys of the wave add together to create stronger more intense light. Where the waves overlap so one line is directly in the midde of the space between two lines is destructive interference, a peak is directly overlapping the valley of the other wave and cancelling it out, making no light. The first place there is constructive interference is the caustic line, the primary rainbow. The second area of constructive interference is the first supernumerary band!

If there were no bands without light, we would not be able to see the other colors between them, thus we woud not see rainbows, instead it would just be a white glow like it is on the inside rim of a primary rainbow made from drops too big to make supernumeraries. Similarly if there are too many different sized drops, they would wash each other out since the interference pattern for each size drop is different.